Quantization in Edge AI – What, Why and How

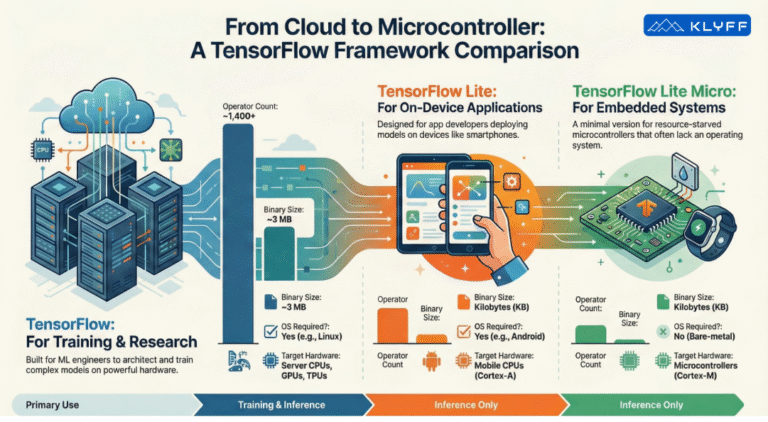
For Edge AI and Embedded engineers overseeing the deployment of Machine Learning (ML) solutions, particularly in the realm of TinyML and embedded systems, the challenge has shifted from model training to inference efficiency. While training demands scale with research complexity, inference cycles scale with the user base. The fundamental constraint in this domain is the limitation of hardware resources—specifically, memory, power, and processing speed.

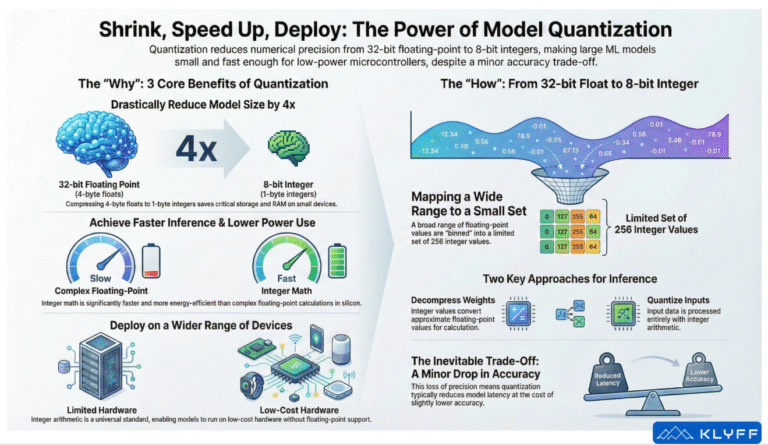
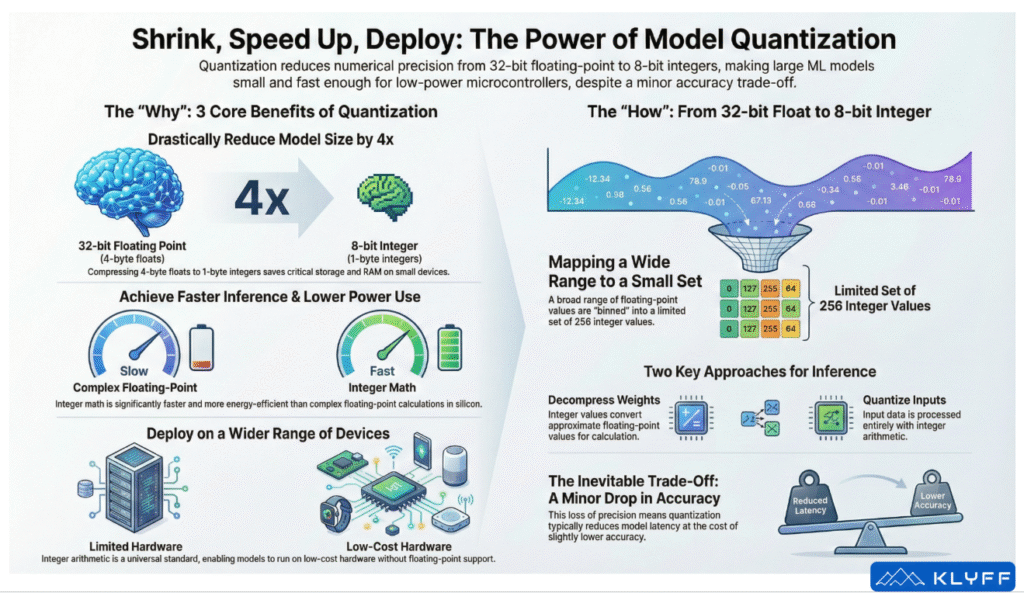
Quantization is not merely a compression technique; it is a critical optimisation paradigm that enables the deployment of complex neural networks onto constrained devices. By reducing the precision of model parameters (typically from 32-bit floating-point to 8-bit integers), organisations can achieve a 4x reduction in model size, significant latency improvements, and broader hardware portability, often with negligible impact on accuracy.

What is Quantization?

At its core, quantization is an optimization process that reduces the precision of the numbers used to represent a model’s parameters. Default TensorFlow models generally represent weights and activations using 32-bit floating-point numbers (float32), which consume four bytes of memory per value.

Quantization compresses these values into a smaller representation, most commonly 8-bit integers (int8), which occupy only a single byte. This transformation results in an immediate 4x reduction in the size of the model’s weights. Look at the example below for a quantized image that uses only 8 colours to represent it. You will notice a loss in accuracy (granularity) in the quantized image.

The Intuition Behind the Math: Neural networks are robust against noise. During training, high precision is required to capture the tiny nudges applied to weights via stochastic gradient descent. However, inference is different. Deep networks act similarly to human perception—just as the human brain ignores “CCD noise” or lighting shifts in a photograph to recognise an object, a neural network can treat the loss of precision from quantization as just another source of noise. Consequently, models can often run with 8-bit parameters without suffering noticeable accuracy loss.

The Triad of Value: Size, Latency, and Portability

For technical decision-makers, the justification for quantization rests on three pillars: Size, Latency, and Portability.

A. Size Constraints (Storage and RAM)

In the embedded world, storage is a hard constraint. A microcontroller might possess only 1 MB of Flash storage. Popular vision models, such as MobileNet, can easily exceed several megabytes in their standard float32 format, making them impossible to store on the device. Quantizing to 8-bit shrinks a 32-bit model by 75%, potentially allowing a previously oversized model to fit within the available flash memory.

The “RAM” Factor: It is crucial to recognize that RAM is not dedicated solely to the ML model. An application is a mix of ML tasks and necessary application logic (the “goo” that holds the app together). The TensorFlow Lite Micro stack, dynamic memory allocation, and non-ML application variables all compete for the same limited RAM (e.g., 256 KB). Reducing the memory footprint of the model frees up critical resources for the rest of the system. Furthermore, fetching 8-bit values requires only 25% of the memory bandwidth compared to floats, reducing bottlenecks on RAM access and improving cache utilization.

B. Latency and Performance

Latency reduction is achieved through the physics of silicon. Floating-point arithmetic is computationally expensive and slow to implement in hardware.

• Integer Arithmetic: May take only 1 to 2 clock cycles.
• Floating-Point Arithmetic: Can take over 10 to 15 clock cycles.

By converting a model to use integer operations, inference speed improves by an order of magnitude. This allows resource-constrained devices to perform significantly more inferences per second, enhancing the user experience. Additionally, hardware accelerators often utilize Single-Instruction Multiple Data (SIMD) operations or Digital Signal Processors (DSP) that are specifically optimized to accelerate 8-bit calculations.

C. Portability and Power

In the embedded ecosystem, power efficiency is king. Floating-point units (FPUs) consume significant power and silicon area. To keep costs and power consumption low, many embedded microcontrollers drop hardware support for floating-point arithmetic entirely.

If a model relies on float32 operations, it cannot run efficiently—or at all—on the subset of hardware that lacks an FPU. By quantizing a network to 8-bit integers, the model becomes portable across a standard baseline of numeric support available on almost all systems. This also translates to power savings; because integer math is “cheaper” to compute, the processor consumes less energy, extending battery life.

The Mechanics of Quantization

One of the most popular quantization techniques is post-training quantization (PTQ). It involves quantizing a model’s parameters (both weights and activations) after training the model.

How do we map a continuous range of floating-point numbers into a discrete set of 256 integers?

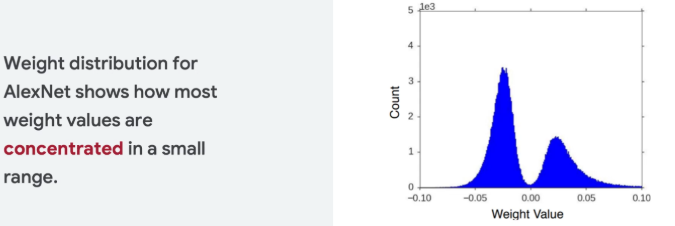
Weight Distribution

Neural network weights tend to be normally distributed and clustered within specific critical ranges. For example, in AlexNet, the weights form a narrow distribution, often appearing as “two ginormous lumps” in a histogram.

• Visualizing the Data: Imagine a histogram of weights. Instead of a broad, flat distribution, the data is concentrated. This allows us to define a minimum and maximum range (e.g., -3.0 to 6.0) and discretize the values inside that range.

The Binning Process

Quantization involves “binning” these floating-point ranges into 8-bit buckets. With 8 bits, we have 256 potential values (0 to 255).

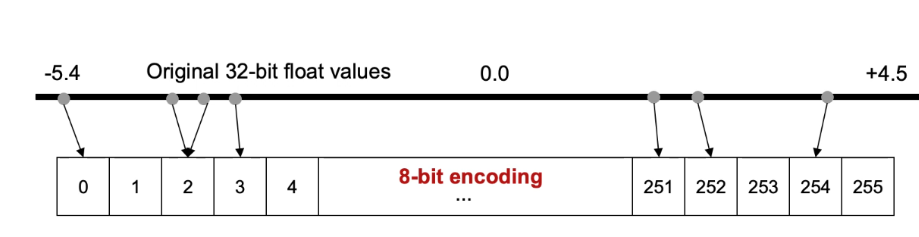
• Mapping: The algorithm stores the min and max for each layer. It then compresses each float value to the closest 8-bit integer in a linear set.
• Example: If the range is -3.0 to 6.0:
  • Byte 0 represents -3.0.
  • Byte 255 represents 6.0.
  • Byte 128 represents approximately 1.5.

This binning allows the system to reconstruct (decompress) the value later. However, this is where the trade-off occurs. Two floating-point values that are very close together might fall into the exact same integer bucket. When decompressed, they will come out as the same value, resulting in a loss of the original resolution.

Implementation Strategies: Post-Training Quantization

There are two primary “legs” or approaches to Post-Training Quantization (PTQ) that architects must understand.

Strategy A: Weight Compression (Storage Optimization)

In this approach, the weights are stored as 8-bit integers to save disk/flash space, but the computation is still performed in floating-point.

1. Storage: The model uses 8-bit integers on disk.
2. Runtime: During inference, the system fetches the 8-bit value and “decompresses” it back into a floating-point number.
3. Compute: The actual multiplication and addition operations are performed using floating-point arithmetic.

Benefit: Reduces storage size (4x).

Drawback: Does not speed up inference because the math is still floating-point. It requires the device to support floating-point arithmetic.

Strategy B: Full Integer Quantization (Speed & Efficiency)

To achieve the latency benefits described earlier, we must eliminate floating-point math entirely.

1. Input Quantization: The input data itself is quantized into a lower precision value.
2. Weight Quantization: Weights are stored as integers.
3. Compute: The inference engine performs integer multiplication and addition.

Benefit: Maximizes speed (integer math is faster), minimizes power, and enables operation on non-FPU hardware.

Code: invoking Quantization in TensorFlow Lite

While the underlying math is complex, modern frameworks like TensorFlow Lite abstract this into API calls. As described in the source materials, developers can instruct the converter to optimize for different characteristics such as size or latency.

The following code illustrates the conceptual workflow described in the source video regarding optimization flags: You can find the code here

import pathlib
converter = tf.lite.TFLiteConverter.from_saved_model(CATS_VS_DOGS_SAVED_MODEL_DIR)

# These options are for converter optimizaitons
# Consider trying the converter without them and
# explore model size and accuracy
# Then...use them and reconvert the model and explore model
# size an accuracy at that point. What differences do you see?

# DEFAULT optimizes for both size and latency, i.e. the model will be smaller and inferencing will be faster
converter.optimizations = [tf.lite.Optimize.DEFAULT]    # Uncomment this line for Model 2 and Model 3

# Let us try full integer quantization
def representative_data_gen():                          # Uncomment the following 5 lines for Model 3
    for input_value, _ in test_batches.take(100):
        yield [input_value]
converter.representative_dataset = representative_data_gen
converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS_INT8]

tflite_model = converter.convert()
tflite_models_dir = pathlib.Path("/tmp/")

tflite_model_file = tflite_models_dir/'model3.tflite'
tflite_model_file.write_bytes(tflite_model)
# This will report back the file size in bytes
# model 1 - 8874204
# model 2 - 2508336 with default optimizations at the time of converting
# model 3 - 2711688

To achieve Full Integer Quantization (Strategy B), the system requires a “representative dataset” to determine the dynamic ranges of activations (the intermediate outputs of neurons). This allows the converter to calculate the min/max values for all variable data flowing through the network, ensuring that inputs and outputs can also be processed as integers.

import os

saved_model_size = sum(os.path.getsize(os.path.join(dirpath, filename)) for dirpath, dirnames, filenames in os.walk(CATS_VS_DOGS_SAVED_MODEL_DIR) for filename in filenames)
print(f"SavedModel directory size: {saved_model_size / (1024*1024):.2f} MB")

tflite_model_size = os.path.getsize(tflite_models_dir/'model1.tflite')
print(f"TFLite model file size without optimizations: {tflite_model_size / (1024*1024):.2f} MB")

tflite_model_size = os.path.getsize(tflite_models_dir/'model2.tflite')
print(f"TFLite model file size with default optimizations: {tflite_model_size / (1024*1024):.2f} MB")

tflite_model_size = os.path.getsize(tflite_models_dir/'model3.tflite')
print(f"TFLite model file size with quantization into INT8: {tflite_model_size / (1024*1024):.2f} MB")

SavedModel directory size: 18.90 MB
TFLite model file size without optimizations: 8.46 MB
TFLite model file size with default optimizations: 2.39 MB
TFLite model file size with quantization into INT8: 2.59 MB

As we can see in the example above, a TensorFlow model has a size of 18.9MB. Once this is converted to a TFLite model, it has a size of 8.5MB

The DEFAULT optimization brings the size down by 4x to 2.4 MB

Full integer quantization is slightly larger at 2.6 MB

The Trade-offs: “No Free Lunch”

Quantization is an exercise in compromise. While we gain speed and space, we sacrifice precision.

• Accuracy Loss: When you discretize weights, you lose resolution. The graph of accuracy versus latency shows a clear trend: as you move to the left (lower latency/faster speed), the point also drops slightly (lower accuracy).
• Resolution Limits: Sometimes floating-point values are so precise that multiple distinct values map to the same integer bin. This loss of information is permanent.

However, this trade-off is often acceptable in commercial applications where the gains in performance, latency, and memory bandwidth are justifiable against a minor drop in predictive confidence.

Beyond Weights: Total Network Quantization

While this article focuses heavily on weights (because they dominate storage), architects should note that quantization can be applied to other parts of the neural network:

• Biases: Every neuron computation involves a bias vector.
• Activations: The data flowing out of neurons.
• Channels: Different granularity of quantization.

There is no “silver bullet”; different quantization schemes offer different trade-offs, but quantizing weights is the most common starting point due to their impact on storage.

Conclusion

For Edge AI engineers designing for the edge, quantization is not optional—it is a requirement. It is the bridge between massive, research-grade neural networks and the reality of 1 MB microcontrollers.

By moving from 32-bit floating-point to 8-bit integer representations, we align our software with the physical realities of embedded hardware:

1. Size: Fitting 5 MB models into 1 MB flash.
2. Speed: Utilizing single-cycle integer math instead of multi-cycle float math.
3. Portability: Running on low-power, low-cost silicon without FPUs.

For more details on the internals, refer to this excellent article